Replacing malloc with rand
The malloc function is fairly simple.
Either give me a pointer to some memory I can use or give me NULL if I’ve asked for too much.
And, on linux that’s exactly what happens:
int main() {
int *ptr;
ptr = malloc(1000); // ptr = 0x563bd6707260
ptr = malloc(1000000000000); // ptr = 0x0
printf("%p\n", ptr);
}
However, something interesting happens when you try this on a mac:
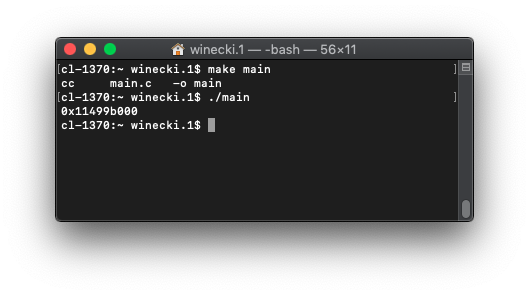
It works…
but why? Surely this 8 GB Mac isn’t going to find a free terabyte lying around.
Clearly it’s mistaken, and as soon as we write to it it’ll segfault:
for(size_t i = 0; 1; i++) {
ptr[i] = 0;
}
And… it got to 64GB before getting killed:

It didn’t even put a dent in the system resources:

Okay, so it looks like either macOS is discarding writes to memory, or it realized it’s all zeros so it’s compressing them. Lets try again with some higher entropy data:
for(size_t i = 0; 1; i++) {
ptr[i] = rand();
}
It still gets to 64GB, but not without swapping to disk:


So it looks like malloc actually did return a terabyte of virtual address space, even if we won’t be able to use all of it.
It’s pretty clear what’s happening here, macOS is just filling in the memory pages when we need them, not when we get assigned them. Or as it’s known formally, demand paging. There are plenty of benefits to this type of memory management, especially for laptops. This is what lets a relatively low spec Macbook run Docker, Chrome, and a handful of Electron apps all at once while still being usable.
So, if a terabyte works, how large can we go? It’s a 64 bit system, so \(2^{64}\), right?
Well, modern x86_64 CPUs only support 48 bit memory address, since 256TB is enough for most people. And sure enough, allocating 100TB works perfectly fine, but trying to allocate a petabyte causes something to break:
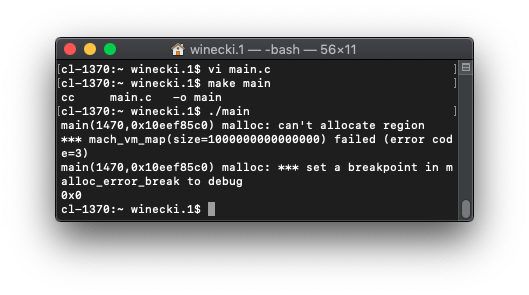
But this also has one other benefit, it lets you try out how programs could run with huge amounts of RAM.
rand() as an allocator
If you have enough memory in a system you can just pick some number at random and hope it works, right?
To put this theory to the test I pulled a copy of Redis, an in-memory database, and started replacing it’s allocator.
Redis uses one of three allocators, set at compile-time, and wraps them in a custom wrapper as zmalloc, so changing one place would change it for the whole project.
To start, lets get 100TB, and then just pick a spot somewhere in that:
void *zmalloc(size_t size) {
// printf("zmalloc size=%lu\n", size);
static void *block = 0;
if(!block) {
block = malloc(100000000000000);
}
size_t rand64 = ((size_t) rand() << 32) | ((size_t) rand());
rand64 %= 100000000000000;
return block + rand64;
}
There’s also calloc, but let’s assume there are zeros there anyway:
void *zcalloc(size_t size) {
return zmalloc(size);
}
realloc can get a little weird, so let’s try to keep most of the original behavior:
void *zrealloc(void *ptr, size_t size) {
if(size == 0 && ptr != NULL) {
zfree(ptr);
return NULL;
}
if (ptr == NULL) return zmalloc(size);
return ptr;
}
And finally,
void zfree(void *ptr) {
return;
}
So does it work? Yes!
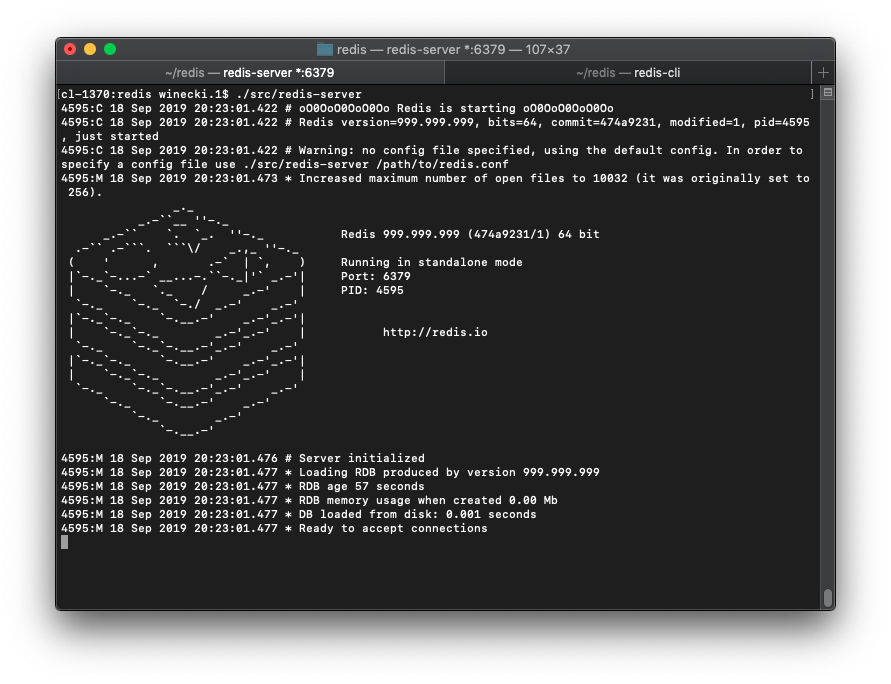
It even accepts user connections through redis-cli!
Sure, once you try to run a remote command you get a segfault, but you can’t win them all.
It takes +13000 zmalloc calls to get a server running, and it works!
Now let’s see if it passes tests:
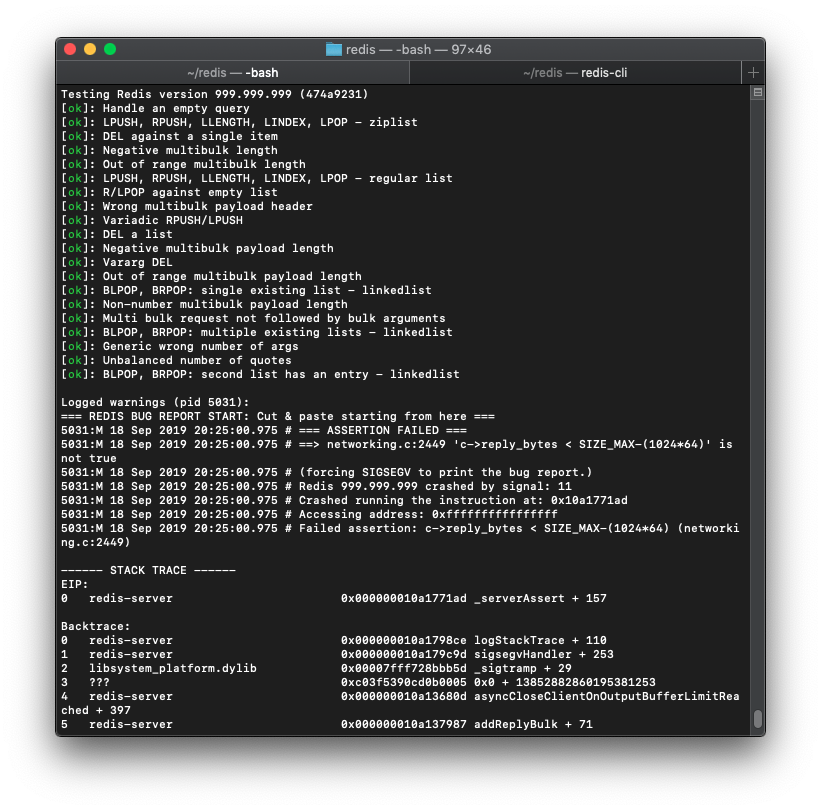
Hey, passing the first 20 tests, not too bad! There were some data structure tests in those. It didn’t even fail due to a segfault or anything, it just can’t check how large an allocated block was.
Did that really need 100TB of space?
Couldn’t this have worked with just 8GB?
If the goal is to avoid memory collisions, then what is the chance a duplicate pointer gets returned? This exact situation gets covered by the birthday problem. If we have \(k = 50000\) separate allocations and \(n=\text{100 trillion}\) then the chance of a collision can be found with this formula:
\[1-\left(\frac{n-1}{n}\right)^{\frac{(k^2-k)}{2}}\]Given 100TB of address space, the chance of a collision across 50k allocations is 0.00125%. With 8GB it’s 14.47%. And this only accounts for pointer collisions, much more address space gets used.
And all of this is before considering that rand() isn’t exactly cryptography-grade randomness either.
So, if you are picking your pointers at random, at the very least, taking advantage of demand paging gives you a little more peace of mind.